Today I’m happy to announce another guest post; this time Sean Westfall is going to give us an extensive run down on Template Haskell. Template Haskell is a somewhat contentious extension, but still remains an important tool in the Haskellers toolbox, allowing us to solve problems concisely. Sean’s gone in to a great amount of detail in this post, and you’ll be sure to take something away with you.
Template Haskell is an extension of Haskell 98 that allows for compile-time metaprogramming – allowing one to directly convert back and forth between concrete Haskell syntax and the underlying abstract syntax tree (AST) of GHC. Anyone familiar with Lisp’s macro system will immediately recognize the similarities – though in Haskell, specific datatypes are used to represent an AST that is used to draw and splice back in code fragments. The ability to generate code at compile time allows one to implement macro-like expansions, polytypic programs, user directed optimization (such as inlining), and the generation of supporting data structures and functions from existing data structures and functions.1
In brief, Oxford brackets [| and |] are used to get the abstract syntax tree for the enclosed expression and ‘splice’ brackets $( and ) are used to convert from the abstract syntax tree back into Haskell. The Quotation Monad is used to give unique names to the parsed tokens from the supplied Haskell code, and reification can be used to look up the name, type, constructor, and state of expression, and as well as the AST of Haskell types.2
Template Haskell was introduced by Tim Sheard and Simon Peyton Jones in their paper “Template Meta-Programming for Haskell” (The original paper can be found here) in 2002, though its changed quite a bit since (see here). It was inspired by C++ templates, though TH is functionally more similar to a macro system. Quasiquotation is often used in conjunction with Template Haskell, but makes up a pretty big section, so I will only briefly describe it here. Only another full article of its own, could do quasiquotation justice.
In the wild, Template Haskell is used extensively by Yesod for routing and HTML template binding.3 Outside of Haskell, compile-time metaprogramming is used for the creation of Domain Specific Languages (DSLs), typically in the domains of testing and modeling, and generative metaprogramming (compile-time or not) for object relational mapping, typically for mapping database schemas to non-compiled code. And within Lisp, which is famous for it’s macro system, metaprogramming is used to create syntax extensions (syntactic sugar), such as the syntax used in lisp comprehensions.4
All code in this guide was executed with GHCi version 7.6.3 and Template Haskell version 2.9.0.0
To get started, start up GHCi with the Template Haskell extension by including -XTemplateHaskell, then load the AST datatypes:
$ ghci -XTemplateHaskell
Prelude> :m + Language.Haskell.TH
Prelude Language.Haskell.TH>To see the AST syntax of some Haskell code insert valid Haskell syntax into oxford brackets and run it through runQ which stands for the Q monad (quotation monad):
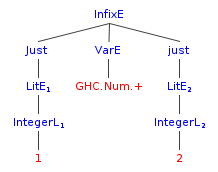
> runQ [| 1 + 2 |]
InfixE (Just (LitE (IntegerL 1))) (VarE GHC.Num.+) (Just (LitE (IntegerL 2)))If you parse through the parentheses you’ll see the return expression forms a tree – an abstract syntax tree!

Checkout the lift class source, which is what’s being invoked by the oxford brackets. The Language.Haskell.TH.Syntax contains the definitions of all the types used in the AST. Using these types, it’s possible to construct any fragment of the Haskell language. Have a look at the Lit data type as an example. Lit stands for literal,
data Lit = CharL Char
| StringL String
| IntegerL Integer -- ^ Used for overloaded and non-overloaded
-- literals. We don't have a good way to
-- represent non-overloaded literals at
-- the moment. Maybe that doesn't matter?
| RationalL Rational -- Ditto
| IntPrimL Integer
| WordPrimL Integer
| FloatPrimL Rational
| DoublePrimL Rational
| StringPrimL String -- ^ A primitive C-style string, type Addr#
deriving( Show, Eq, Data, Typeable )tokens represented by it make up literals defined throughout your syntax in the AST, as you can see in our example AST above. Within Language.Haskell.TH.syntax, 35 generic data types are declared with the Data.Data module. If you’re curious about what the AST syntax is referring to study the source.
The Q monad handles the expression’s typing via context, and also gives it a unique name by appending an integer at the end of the expression name to handle scoping distinction. Quotations are lexically scoped and the Q monad handles this using it’s naming scheme. (see the user’s guide wiki for a more in depth explanation of TH’s lexical scoping).
Let’s bind the returned AST expression from the example above to Haskell and evaluate it, using the splice brackets:
> $( return (InfixE (Just (LitE (IntegerL 1))) (VarE (mkName "+")) (Just (LitE (IntegerL 2)))))
3Ta da, you converted concrete Haskell to AST and then evaluated it. Though, as you can see, identifiers have to be defined with the mkName type in the AST to evaluate properly.
It’s possible to avoid having to modify the AST to splice it back, but you’ll have to bind it to a variable, as my next example illustrates:
In this example, the Fibonacci sequence is generated using zipWith:5
let fibs :: [Integer]
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
let fibQ :: Int -> Q Exp
fibQ n = [| fibs !! n |]Now run $( ... ) to excute the expansion:
> $(fibQ 22)
17711TH splices in the expression that fibQ represents along with the variable (that is fibs !! n).
Note, expressions and splices can be nested:
> $(runQ [| fibs !! $( [| 8 |]) |])
21I’ll explain TH’s syntax next – but after, I’ll show some more impressive examples that show the possibilities of splicing and ASTs.
Template Haskell quotation expression come with 4 different parser types, and an extensive 5th optional type that allows one to define their own types of quotations, called quasi-quotations.
[| ... |], or [e| ... |], generates expression AST syntax; it has the type Q Exp.
> runQ [| 1 + 2 |]
InfixE (Just (LitE (IntegerL 1))) (VarE GHC.Num.+) (Just (LitE (IntegerL 2)))[d| ... |], generates a list of top-level declaration AST sytnax; it has the type Q [Dec].
> runQ [d|x = 5|]
[ValD (VarP x_4) (NormalB (LitE (IntegerL 5))) []][t| ... |], generates a type AST syntax; it has the type Q Type.
> runQ [t|Int|]
ConT GHC.Types.Int[p| ... |], generates a pattern AST syntax; it has the type Q Pat.
> runQ [p|(x,y)|]
TupP [VarP x_5,VarP y_6]Custom “quasi-quotations”, have the form ["quoter"| ... |]. The “quoter” can be anything except e, d, t, and p, and the token cannot contain spaces. Though, all GHC is doing is determining which parser to use based on the context within the oxford brackets.6
Quasi-quotations is a big second part to meta-programming. They’re essentially what makes it possible to write DSLs. I’m not going to cover it here since this guide is pretty long as it is, but if you’re interested, there are many guides to using quasi-quotations, find them here, here, and here (this one assumes you’re familiar with Parsec parsing).
An important restriction on Template Haskell to remember is when inside a splice you can only call functions defined in imported modules, not functions defined elsewhere in the same module. Quotations and splice have to be defined in separate modules, otherwise you’ll see this error:
GHC stage restriction:
`...' is used in a top-level splice or annotation,
and must be imported, not defined locallyThough, if you’re just binding variables in GHCi with let, you don’t have to worry about this – only when you’re compiling Haskell.
You’re probably wondering if you can evaluate a Q expression the other way, to see what the splice is evaluating. Of course you can – run runQ(Q exp) >>= putStrLn.pprint to see what an expression with a Q Exp type will evaluate to:
> let myExp :: Q Exp; myExp = runQ [| 1 + 2 |]
> runQ(myExp) >>= putStrLn.pprint
1 GHC.Num.+ 2If you want to see the expansion of splices, use the flag -ddump-splices when starting GHCi : ghci -XTemplateHaskell -ddump-splices.
Now let’s test it on another fun example with primes:7
let isPrime :: (Integral a) => a -> Bool
isPrime k | k <=1 = False | otherwise = not $ elem 0 (map (mod k)[2..k-1])
let nextPrime :: (Integral a) => a -> a
nextPrime n | isPrime n = n | otherwise = nextPrime (n+1)
-- returns a list of all primes between n and m, using the nextPrime function
let doPrime :: (Integral a) => a -> a -> [a]
doPrime n m
| curr > m = []
| otherwise = curr:doPrime (curr+1) m
where curr = nextPrime n
-- and our Q expression
let primeQ :: Int -> Int -> Q Exp
primeQ n m = [| doPrime n m |]> $(primeQ 0 67)
<interactive>:18:3-13: Splicing expression
primeQ 0 67 ======> doPrime 0 67
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67]Try it on a nested expression, to really see how useful the dump-splices flag is:
> $(primeQ ($(primeQ 0 23) !! 3) 167)
<interactive>:20:13-23: Splicing expression
primeQ 0 23 ======> doPrime 0 23
<interactive>:20:3-34: Splicing expression
primeQ ($(primeQ 0 23) !! 3) 167 ======> doPrime 7 167
[7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167]-ddump-splices and >>= putStrLn.pprint should come in handy when debugging.
Now for probably, what I consider to be the hardest aspect of Template Haskell to understand – reification.
Reification allows one to query the state of Haskell Names and get information about them. Specifically, reify returns a data type called info – which returns data in a specific format on any Name in Haskell, where the format and information depends on whether it’s being interpreted in a type context or an expression context.
TH introduces two new identifiers specifically for reification: Prefix Names to be evaluted in an expression context with a single quote, and prefix Names to be evaluated in a type context with a double quote. Though, Names must be interpretable within those contexts to be reified. (If you intend to use reify on expressions, don’t use quotes in the names of those expressions – otherwise it won’t parse correctly.)
To use reify on a type, use double quotes:
> $(stringE . show =<< reify ''Bool)
"TyConI (DataD [] GHC.Types.Bool [] [NormalC GHC.Types.False [],NormalC GHC.Types.True []] [])"Reifying a type returns the AST as represented by TH, here’s the AST in a diagram of the boolean type from above:
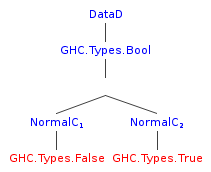
The AST of a simple primitive type like Bool produces a small tree, but when used on types deeper down the module chain, relatively large ASTs will be generated. Try reify on ''Lit or ''Exp to know what I mean, though reify can work on any Haskell type.
To reify an expression, use single quotes, here’s an example with our primeQ expression from above:
> $(stringE . show =<< reify 'primeQ)
"VarI primeQ_1627395913 (AppT (AppT ArrowT (ConT GHC.Types.Int)) (AppT (AppT ArrowT (ConT GHC.Types.Int)) (AppT (ConT Language.Haskell.TH.Syntax.Q) (ConT Language.Haskell.TH.Syntax.Exp)))) Nothing (Fixity 9 InfixL)"As you can see info returns different information depending on whether it’s a type or an expression. A type returns its structure in TH’s AST semantics. An expression returns information regarding its name, type, it’s constructor, and it’s fixity.
Use reification of expressions to extract the types associated with the construction of an expression, then reify those types to get its structure in an AST. This allows one to generate the AST of any data type in Haskell – no matter how deep into Haskell it gets.
Reification is very useful from the standpoint of what one can do with an AST to draw and splice back in code fragments within a programming language. Below, in Examples, the second example shows how one can use reify to extract the types from a record’s constructor to write a generic Show function that can generate a Show for any record.
A good example to show what one can do with Template Haskell is a type safe Haskell version of c’s printf function (from stdio.h):8
Main.hs
{-# LANGUAGE TemplateHaskell #-}
-- Import our template "printf"
import PrintF (printf)
-- The splice operator $ takes the Haskell source code
-- generated at compile time by "printf" and splices it into
-- the argument of "putStrLn".
main = do
putStrLn $ $(printf "Hello %s %%x%% %d %%x%%") "World" 12
putStrLn $ $(printf "Hello %s %s %s %d") "Russian" "with" "Love" 5000PrintF.hs
{-# LANGUAGE TemplateHaskell #-}
module PrintF where
-- NB: printf needs to be in a separate module to the one where
-- you intend to use it.
-- Import some Template Haskell syntax
import Language.Haskell.TH
-- Possible string tokens: %d %s and literal strings
data Format = D | S | L String
deriving Show
-- a poor man's tokenizer
tokenize :: String -> [Format]
tokenize [] = []
tokenize ('%':c:rest) | c == 'd' = D : tokenize rest
| c == 's' = S : tokenize rest
tokenize (s:str) = L (s:p) : tokenize rest -- so we don't get stuck on weird '%'
where (p,rest) = span (/= '%') str
-- generate argument list for the function
args :: [Format] -> [PatQ]
args fmt = concatMap (\(f,n) -> case f of
L _ -> []
_ -> [varP n]) $ zip fmt names
where names = [ mkName $ 'x' : show i | i <- [0..] ]
-- generate body of the function
body :: [Format] -> ExpQ
body fmt = foldr (\ e e' -> infixApp e [| (++) |] e') (last exps) (init exps)
where exps = [ case f of
L s -> stringE s
D -> appE [| show |] (varE n)
S -> varE n
| (f,n) <- zip fmt names ]
names = [ mkName $ 'x' : show i | i <- [0..] ]
-- glue the argument list and body together into a lambda
-- this is what gets spliced into the haskell code at the call
-- site of "printf"
printf :: String -> Q Exp
printf format = lamE (args fmt) (body fmt)
where fmt = tokenize formatNotice that we had to separate the splicing and the expression definitions in separate modules, as mentioned in the syntax section above.
Compile the following with:
$ ghc --make Main.hs -o mainrunning main will print out:
$ ./main
Hello World %%x%% 22 %%x%%
Hello Russian with Love 5000Now for an example that shows what one can do with reify – a Generic Show that can produce a Show for any record type:9
Main.hs
{- Main.hs -}
module Main where
import Derive
data T = A Int String | B Integer | C
$(deriveShow ''T)
main = print [A 1 "s", B 2, C] -- prints exactly <<[A 1 "s",B 2,C]>>Derive.hs
{- Derive.hs -}
module Derive where
import Language.Haskell.TH
import Control.Monad
data T1 = T1
data T2 a = T2 a
deriveShow t = do
-- Get list of constructors for type t
TyConI (DataD _ _ _ constructors _) <- reify t
-- Make `show` clause for one constructor:
-- show (A x1 x2) = "A "++show x1++" "++show x2
let showClause (NormalC name fields) = do
-- Name of constructor, i.e. "A". Will become string literal in generated code
let constructorName = nameBase name
-- Get variables for left and right side of function definition
(pats,vars) <- genPE (length fields)
-- Recursively build (" "++show x1++...++"") expression from [x1...] variables list
let f [] = [| "" |]
f (v:vars) = [| " " ++ show $v ++ $(f vars) |]
-- Generate function clause for one constructor
clause [conP name pats] -- (A x1 x2)
(normalB [| constructorName ++ $(f vars) |]) [] -- "A "++show x1++" "++show x2
-- Make body for function `show`:
-- show (A x1 x2) = "A "++show x1++" "++show x2
-- show (B x1) = "B "++show x1
-- show C = "C"
showbody <- mapM showClause constructors
-- Generate template instance declaration and then replace
-- type name (T1) and function body (\x -> "text") with our data
d <- [d| instance Show T1 where
show x = "text"
|]
let [InstanceD [] (AppT showt (ConT _T1)) [FunD showf _text]] = d
return [InstanceD [] (AppT showt (ConT t )) [FunD showf showbody]]
-- Generate n unique variables and return them in form of patterns and expressions
genPE n = do
ids <- replicateM n (newName "x")
return (map varP ids, map varE ids)Compile the following with:
$ ghc --make Main.hs -o mainrunning main will print out:
$ ./main
[A 1 "s",B 2,C]This guide was for the most part written from collecting information written in other guides on Template Haskell, quasi-quoting, and Lisp macros – from online, wiki, and academic sources. Please check my bibliography to see where what came from what so credit can be properly given where it’s due.
Meta-programming is a powerful programming technique that can allow for the generation of user generated syntax extensions and DSLs. This is useful in that it can allow a programmer to generate custom code generating syntax extensions without otherwise having to change the core language. Template Haskell in particular is especially powerful over similar programming language constructs (i.e. The C Preprocessor, Lisp’s Macro system) in that it makes use of ASTs, reification (through a specific function), and – much in the spirit of Haskell – type-safety. The examples presented above only scratch the surface of what’s possible with reification – imagine the ability to construction entire systems, and then use reify to build ASTs, then swap in and out entire modules, entirely with the use of Template Haskell.
Some questions that have arisen within me from writing this article are: What are the limits of TH’s data type system? Is it truly possible for TH to represent all of Haskell with the finite set of data types written into the module? Is it possible for future language features to defy this set? What are the limits of meta-programming – TH, macros, and similar meta-prorgramming constructs make it possible to write code that writes code – but are there limits to this – is it possible to write a macro that can generate a macro, and so on indefinitely?
Don’t forget to checkout the API. Everything you need to know, you can for the most part find in the source. Also TH does in fact have bugs, check the issue tracking page if you’re dealing with a known issue: see here.
(The MIT License)
Copyright (c) 2014 Sean Westfall
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the ‘Software’), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED ‘AS IS’, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Tim Sheard and Simon Peyton Jones, “Template meta-programming for Haskell,” ACM SIGPLAN 2002 Haskell Workshop 3 (October 2002): 1-6, doi: 10.1145/581690.581691↩︎
The Glorious Glasgow Haskell Compilation System User’s Guide, Version 7.8.3, 2007↩︎
Greg Weber, Code that writes code and conversation about conversations, 2011:↩︎
Peter Seibel, Practical Common Lisp (Apress, 2005)↩︎
Mike Ledger, “A look at QuasiQuotation,” 2012.↩︎
Sami Hangaslammi, Basic Tutorial of Template Haskell, 2011:↩︎
Peter Seibel, Practical Common Lisp (Apress, 2005)↩︎
Template Haskell, Haskell Wiki, last updated October 2014: https://www.haskell.org/haskellwiki/Template_Haskell↩︎